似乎五子棋流行一种思想,认为黑棋优势是因为黑多了一个子,且优势会随着子数增多而不断削弱。但我们知道26种开局都符合该思想的要求,但26开局的优势变化却很难说符合该思想的结论。当然,几乎人人都可以找到理由为该思想进行辩护,诸如a黑必胜故无优势削弱,黑1、3子距离太远形成弃子,棋子间搭配关系,人为行棋失误等,而且这些理由基本都是正确的。
几年前我也曾思考过这个问题,但不大接受这些理由,因为我认为这些理由不利于科学全面地认识问题,这里就不做太多的专业说明。然而,黑棋确确实实多了个棋子,若少了这个子黑棋也确实优势不起来,思考陷入困境。
直到有一天,sosei大师讲课时说道:五子棋就是玩连接的。我突然豁然开朗,虽然我们嘴上称下棋下棋,但实际在棋盘上起最直接作用的是棋子带来的绑定着的4条线(连接),而不是棋子本身。
由于受到sosei思想启发,我尝试换种方式来表述五子棋(为了避免禁手表述困难,这里指无禁五子棋):在15*15棋盘,双方轮流“走”以某点为中心的4条长度9格的线(2条直线2条斜线),中心点不允许重叠。一方在棋盘上任意连续5格的线重叠5次为胜。
虽然换了种表述方式,但本质还是五子棋,这种表述方式意义在于使基础变量变得清晰:15棋盘(盘端位置),轮流,中心点不重叠,绑定着的,4条长度9格的线(4条线)。
PS:我们知道任何一种棋类,或者说任何一个事物最基本最底部的规则一旦被修改,对整体影响是巨大的。科学实验原理就是在其他变量不变的情况下改变某个变量来观察结果的变化。
先谈“绑定”。按常态(正常的五子棋规则)中心点绑定着4条线,4条线只能位于中心向棋盘8个方向延伸。
假如取消“绑定”规定的话,相当于每回合让你在棋盘上放4条不同方向的线,线的位置由你控制(同方向的线中心不可重叠,异方向线同色可重叠异色不可重叠)。几轮测试轻松发现在该假设下,只要不失误任何一方都不可能取胜,连连续3格线重叠3次都不可能,哪怕无限棋盘亦如此。因为防守效率可以轻松达到100%。
再假设取消“绑定”且允许线方向任意的话,相当于由你任意控制4条线的位置及方向。几轮测试则发现在该假设下,先行绝对必胜。方法:第1回任意摆3个方向以上,无论对方如何防御,之后将4条线集中在同一线上必能达到连续5格5次重叠(即5连)。
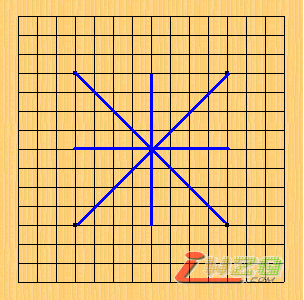
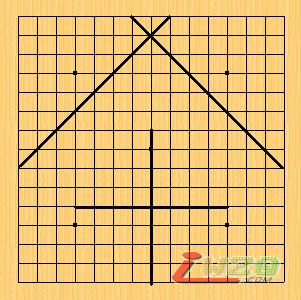
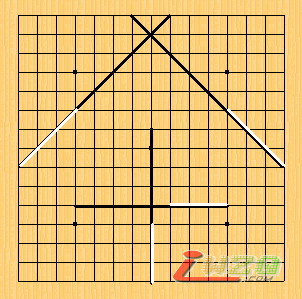

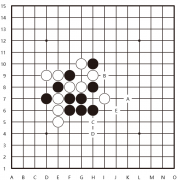
PS:绑定情况下4条线方向位置固定如图1;解除绑定位置任意但方向固定如图2;在此假定下,白可以轻松跟着黑,形成绝对防御;黑甚至要连续3格线3次重叠都不行(无法3连);在假设2下,第1回随意摆4条线,之后无论如何防御,之后将4条线集中一线即可连续5格线5次重叠I,其他4线分别由青,浅蓝,深蓝,紫色表示。
虽然假设荒谬,但实验结果却大大出乎我的意料,从未被关注过“绑定”规定居然对整个五子棋起到如此巨大的影响。之后不得不反思,为什么不改变其他规则单单取消“绑定”会造成如此巨大影响?不难发现,在取消“绑定”下的每一条线都将被完全利用,即每回合的利用率都达到100%;但在正常规则下行棋,通盘下来达到100%利用的棋子仅占少数,大多是75%,50%,25%的点,即便走出进攻或防守的妙手,利用率也难超过75%,而在一方VCT防守方的几个子利用率低至接近25%。
由此,我们不得不对线的利用率引起重视。由于正常规则线利用率受“绑定”影响,因此很容易分支出线的分布、搭配、级别等参数思想。并在一定棋谱统计下可以发现这些参数随着棋局发展呈现出规律性变化,总体上是进攻方线利用率提高,线分布集中化,搭配加强,级别上升,防守方则相反……(建议自己摸索)
至此,假如有人问“如何扩大优势”,某种程度可以等价于“如何提高线的利用率等参数”这样的形象表述。最后回到本文开头的问题:黑棋确实多了一个子,但并不是影响对局优势的直接因素;对局优势更多与线参数互成映射,而线参数能出现规律性变化的主要原因在于先手的利用,最后黑多一子往往是黑拥有先手的直接原因。然而这些并非最重要的~~
转载请注明出处。

 相关文章
相关文章

 精彩导读
精彩导读




 热门资讯
热门资讯 关注我们
关注我们

